Minimal increase counting bloom filter
TL;DR A simple way to reduce overestimations in counting Bloom filters.
Context
Bloom filters are probabilistic data structures used to test whether an element is a member of a set. A Bloom filter is an array of m bits, initially all set to 0. It uses multiple (k) hash functions to map any element to k addresses in the array. When inserting an element x, all the k bits corresponding to the k hash values of x are set to 1.
When checking the membership of an element x, if any of the k corresponding bits is 0, the element is absent. Otherwise, it is reported as present, although this might be a false positive since the k bits may have been set to 1 by other inserted elements.
Counting Bloom filters [1] extend Bloom filters by using b bits per address instead of just one. This allows 1/ elements to be added and removed dynamically, and 2/ elements to be associated with their abundance (up to 2^b-1). When an element is added, the counters at all the k positions determined by the hash functions are incremented. To remove an element, the same counters are decremented.
When an element x is queried, the reported abundance associated with this element is equal to the minimum value stored at its k corresponding addresses. Similar to false positives in Bloom filters, overestimations can occur in counting Bloom filters.
Counting Bloom filter variants
There are numerous clever variants of the counting Bloom filter data structure. A comprehensive overview is provided in [2], which also introduces an interesting idea to limit overestimations.
These variants all have their pros and cons (as does the method I propose here). They often involve sophisticated algorithmic and/or hardware techniques.
What I propose: “the minimal increase counting Bloom filter”
While preparing a lecture about counting Bloom filters, I wondered why “When an element is added, the counters at all the k positions determined by the hash functions are incremented”. The key word here is “all”. Let me explain with an example using the classic counting Bloom filter.
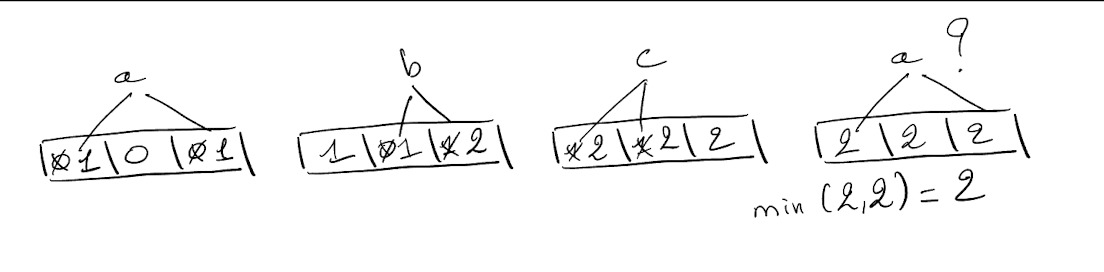
In this example with k=2, we inserted a, b, and c. The reported value of a is 2, while it was inserted only once. It is overestimated because other elements, b and c, share addresses with a.
In the “minimal increase counting Bloom filter,” when adding an element x to a counting Bloom filter, only the minimal value(s) corresponding to this element are incremented. The example becomes:
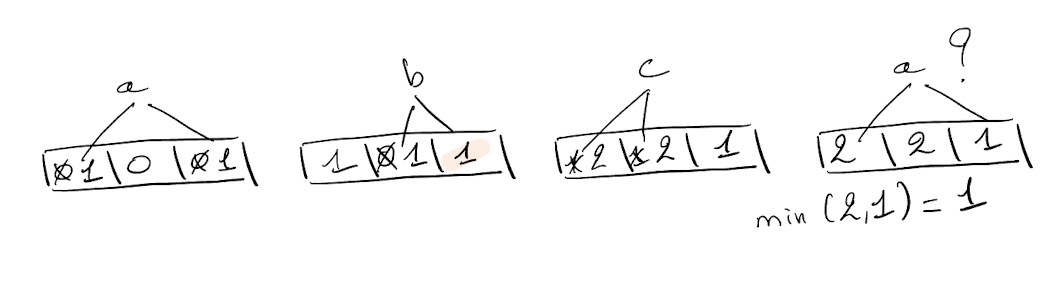
In this example, when inserting b, only the minimal value (0) is incremented, the other one (highlighted), is not modified. The query for a is not overestimated because b and c modified only cells with minimal values.
The rationale is that the value reported for a queried element is the minimum value of all its k counters. Therefore, increasing non-minimal counters when inserting an element only increases the overall overestimation rate.
Simplest code modification
Compared to all existing counting Bloom filter variants, this one is likely the simplest. We only modify the function for adding an element from:
pub fn add<T: Hash>(&mut self, item: &T) {
let indices = self.hash_indices(item);
for &index in indices.iter() {
self.increment_counter(index);
}
}
to
pub fn add<T: Hash>(&mut self, item: &T) {
let mut min_value = self.max_value;
let mut min_hashes = Vec::new();
let indices = self.hash_indices(item);
// collect hash values with minimal counters
for &index in indices.iter() {
let current_value = self.get_counter(index);
if current_value < min_value {
min_value = current_value;
min_hashes = vec![index];
} else if current_value == min_value {
min_hashes.push(index);
}
}
// increase the counter of these hash values only
for &index in min_hashes.iter() {
self.increment_counter(index);
}
}
(though I suspect a Rust expert could optimize this further).
Results
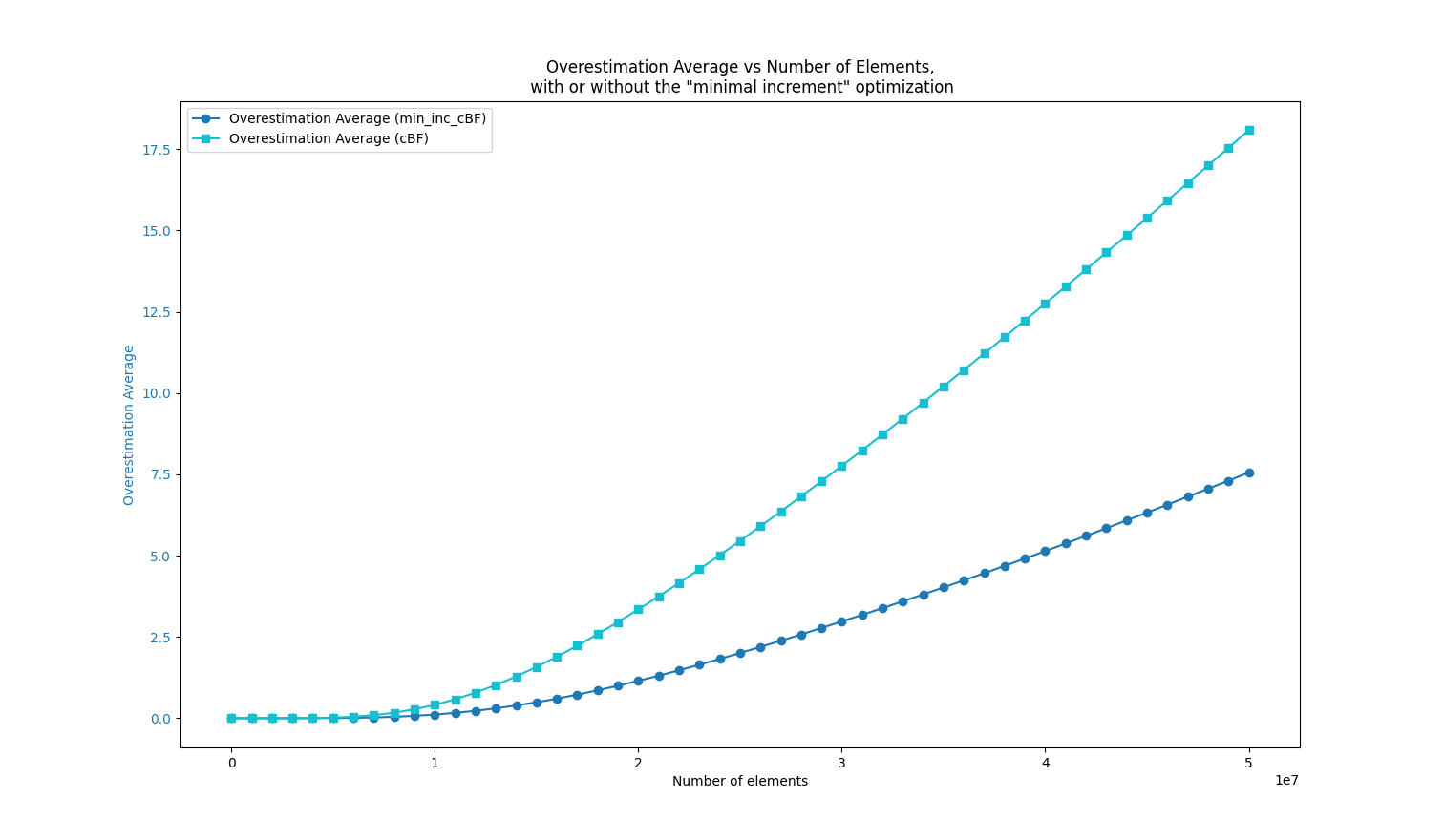
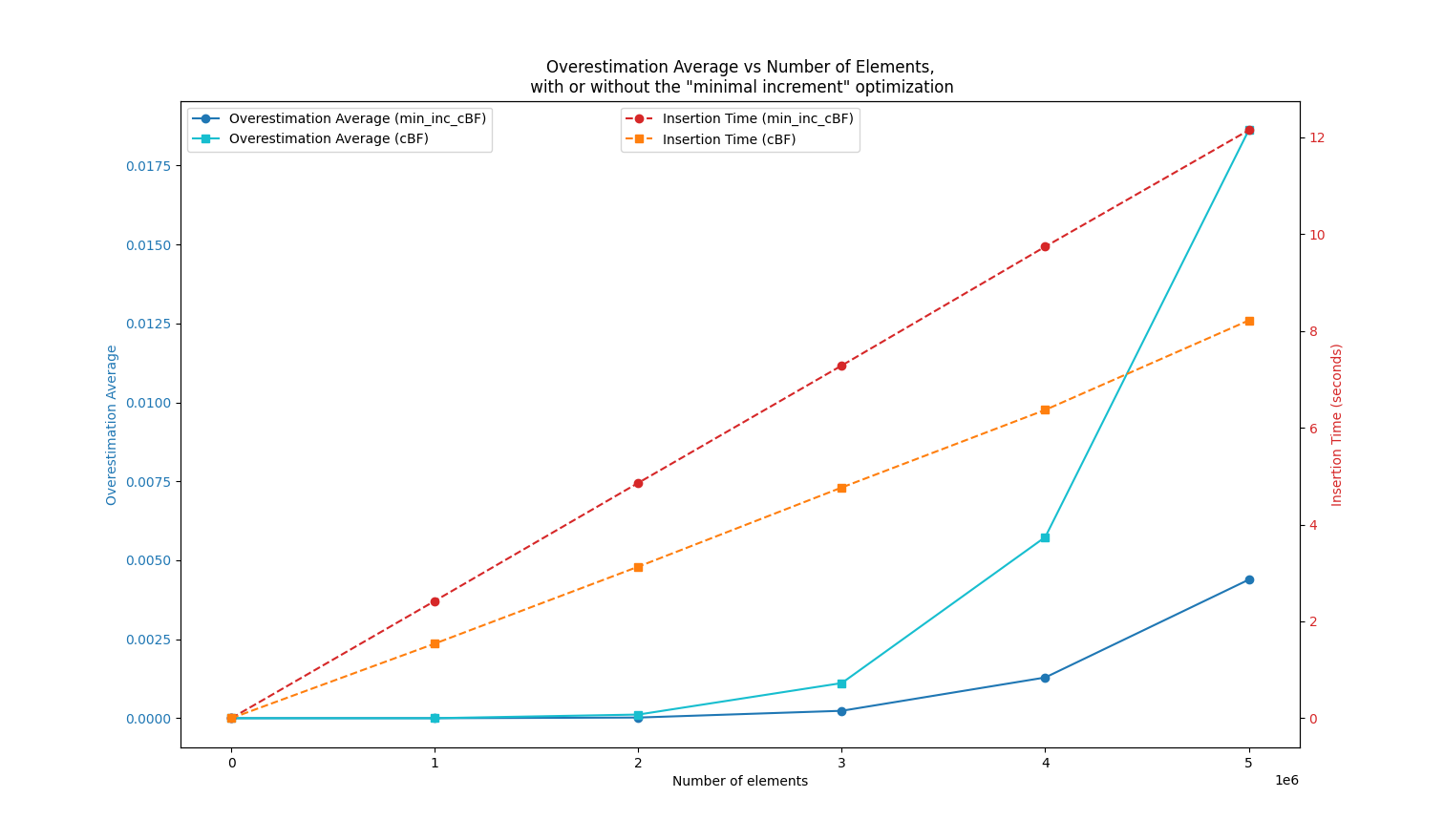
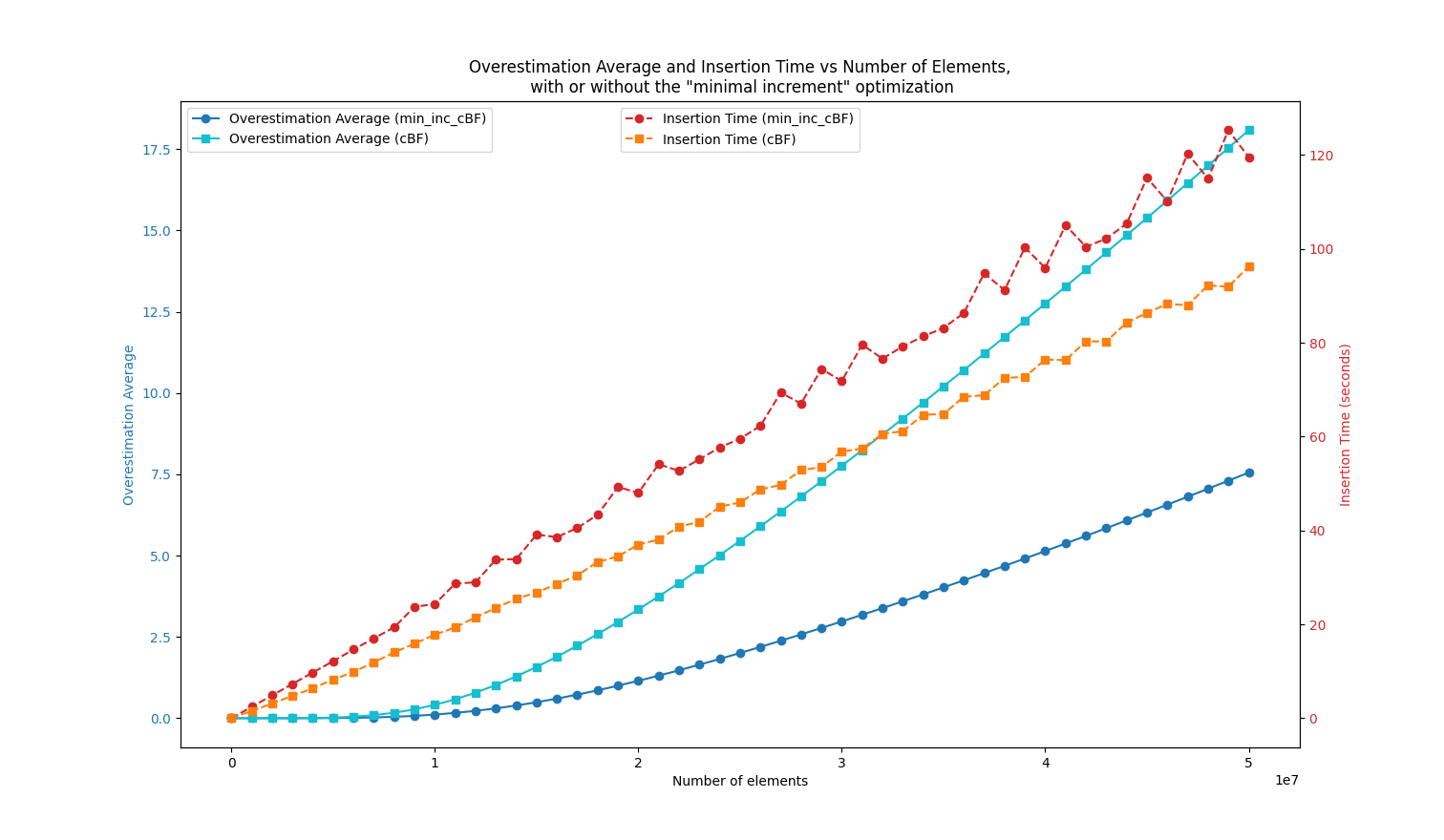In this experiment, I created a Bloom filter with 50 million cells (m=50000000), using k=7 hash functions and storing b=4 bits per cell. I stored an increasing number of elements (random DNA words of length 31) in the filter (x-axis), with each element being inserted between 1 and 10 times (randomly).
The results compare the “minimal increase counting Bloom filter” (min_inc_cBF) with a classical counting Bloom filter (cBF).
The blue curves show the average overestimation rate when querying stored elements (no false positives here).
We can see that the min_inc_cBF overestimation rate is 2 to 3 times smaller than that of the cBF. The orange curves show the indexing time, confirming the first drawback listed below.
Interestingly, for the usual ratio of n/m < 10% (where n is the number of stored elements), the results highlight that this approach performs very well for these typical values, as shown in the zoomed-in view below:
No free lunch
The watchfull readed certainly noticed that this approach introduces some weaknesses.
I identified three main drawbacks:
- Adding an element takes slightly more time, as there are two passes on the counters, and binary-stored values need to be converted to integers.
- Adding an element is not parallelizable (since the minimum must be collected).
- Decreasing the abundance of an element is no longer possible. For example:
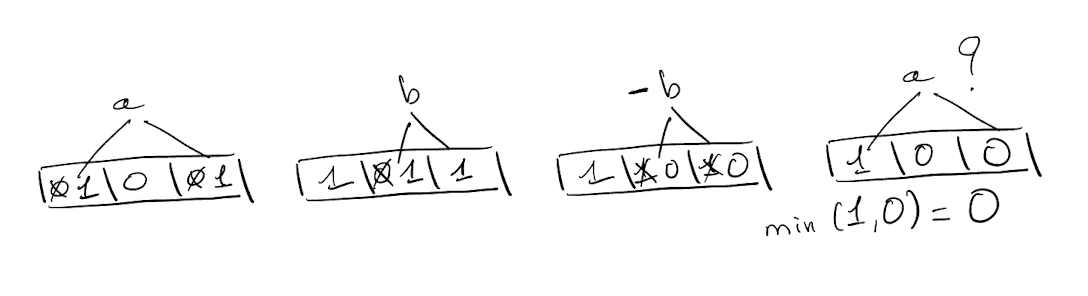In this case, the abundance of a is reported as 0, even though it was inserted once and never removed. - As noted by Antoine Limasset: The final state of the counters depends on the insertion order. For instance, with same hash values as in our previous example, inserting b, then c, then a, generates the filter [2,1,2]. In this case, a decomes overestimated, while the minimal increase strategy still enables to avoid overestimations for b and for c.
Prototype (Rust)
See https://github.com/pierrepeterlongo/minimal_increment_CBF. This prototype enables to reproduce results and to reuse the rust code API.
What’s next?
We should improve the Rust code. Additionally, math enthusiasts could propose a formula to estimate the expected average overestimation rate based on k, m, b, and the number of stored elements and their abundances.
Please contact me if you’re interested: pierre.peterlongo@inria.fr
References
[1] Fan, Li, et al. “Summary cache: a scalable wide-area web cache sharing protocol.” IEEE/ACM Transactions on Networking 8.3 (2000): 281-293.
[2] Rottenstreich, Ori, Yossi Kanizo, and Isaac Keslassy. “The variable-increment counting Bloom filter.” IEEE/ACM Transactions on Networking 22.4 (2013): 1092-1105.
Edited on March 20, 2025